我面试之前是如何准备算法题的
先说说笔者自身的情况:
- 北航本 / 新加坡Top2 硕
- 本科(毕业后)的时候先后在腾讯和字节跳动实习 + 转正工作,经历过大大小小的面试总计大概10来场吧,选择性的粘贴一下之前的面经,可以感觉到不同的公司有不同的面试风格:
阿里支付宝:比较偏重于Java世界,对于New Grad来说八股文的考察比较多,但很基础,电话面试。
腾讯CSIG:比较偏重于 Java,特别是Spring框架,会考察应试者的知识广度,包括消息队列等等,但没有涉及分布式的topic。
字节跳动:字节的面试风格比较清新,直接了当,上来先写题,写完再聊,聊的东西也比较入门级别(对于NG而言),包括:Redis的基本数据结构,MySQL的并发设计;对于搞过分布式系统/分布式存储的同学来说,只要算法没问题,基本秒过。
商汤:商汤面的算法岗,主要是就着Paper 问,只要Paper中的工作是自己做的,把AI框架搞懂了,Pass 应该没啥问题。但是感觉商汤的算法题有点天马行空,事先可能准备不到。
美团:美团面的基础架构,主要做AP系统的应该是,可能我给面试官的感觉比较菜?全程没问我分布式的内容,在聊项目,MySQL聊的比较多,Redis分布式锁。
回到现实:这篇Blog记录了我第一次在新加坡准备面试的刷题路线,因为感觉论坛中热门的Hot200, Top100基本都刷了好几遍了,并且向UC Berkerly / FaceBook 的大佬请教了经验之后,认为分类刷题是一种很好的习惯。准备面试算法,就和准备高中数学期末考试一样,既有广度,也要考察深度,我应对这种考试一般的方式就是分类刷题,每一个类别都需要细致的研究和总结。
下面这个链接是我的刷题记录。
个人力扣刷题记录:leetcode-update
最后还想说一点笔者的拙见:【心态要好】其实面试的过程是双向的,应试者没有必要抱着舔狗或者非要进XX公司不可的心态去面试,而应该将面试看做是一个双向了解和沟通的过程,面试官既是在考察应试者的技术能力,应试者也可以通过面试官的提问路线(是否循序渐进,是否能指出错误,沟通是否顺畅)来评估自己是否适合进入该组工作。
隆重推荐,没收广告费
GitHub整理的LeetCode刷题指南:https://github.com/youngyangyang04/leetcode-master
数组
已掌握:双指针 滑动窗口 前缀和 动态规划
听说过未掌握:线段树
搜索旋转排序数组
都需要在 **O(logN)**的时间复杂度内完成,因此思路都是希望每次迭代排除一半的元素。
解法:对于数组中最后一个元素,在最小值左边的元素,都严格大于最后一个元素,在最小值右边的元素,都严格小于最后一个元素。基于此发现,可以将中间位置与数组最后一个值比较。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int left=0, right=nums.length-1;
while(left<right){
int mid = (left+right)/2;
if(nums[mid] <= nums[right]){
right--;
}else {
left = mid+1;
}
}
return nums[left];
|
是否允许重复并不会影响搜索的结果,所以解法和上面一道题相同。
高亮的部分严格控制了区域内的有序性,根据这个有序性,每次排除掉一半的数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| int left=0, right=nums.length-1;
int last=nums[right];
while(left<=right){
int mid=(left+right)/2;
if(nums[mid] == target) return mid;
if(nums[mid]>last){
if(nums[mid]>target && target>last){
right=mid-1;
}else {
left=mid+1;
}
}
else {
if(nums[mid]<target && target<=last){
left=mid+1;
}else {
right=mid-1;
}
}
}
return -1;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| int left=0, right=nums.length-1;
int last=nums[right];
while(left<=right){
int mid=(left+right)/2;
if(nums[mid] == target || nums[left]==target || nums[right]==target) return true;
if(nums[mid]==nums[right] && nums[mid]==nums[left]){
right--;
left++;
continue;
}
if(nums[mid]>last){
if(nums[mid]>target && target>last){
right=mid-1;
}else {
left=mid+1;
}
}else {
if(nums[mid]<target && target<=last){
left=mid+1;
}else {
right=mid-1;
}
}
}
return false;
|
删除有序数组重复项
O(N)
思路:以不能重复为例,使用快慢指针,slow指针之前的元素都是唯一的,fast之前的元素都被检查过。
1
2
3
| 如果 nums[slow-1] = nums[fast],说明fast这个位置是重复的元素,应该跳过,直接更新fast++
如果 nums[slow-1] != nums[fast],有序性保证了fast位置的元素在slow之前都没有出现过,所以替换nums[slow]=nums[fast], 并且slow++,fast++
|
循环做以上逻辑,直到fast超出原始数组长度,结束。此时slow保存了去重后的数组长度。
并查集
能够求解的问题:
- 判断图中的连通分量 LC547
- 判断是否能够产生二分图 LC785
模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class UnionFind{
int[] parents;
public UnionFind(int nodeNum){
parents = new int[nodeNum];
for(int i=0;i<nodeNum;i++) parents[i]=i;
}
public int find(int node){
while(parents[node] != node){
node = parents[node];
}
return node;
}
public void union(int node1, int node2){
int root1 = find(node1);
int root2 = find(node2);
parents[root1]=root2;
}
public boolean isConnected(int node1, int node2){
return find(node1) == find(node2);
}
}
|
使用注意:
背包问题的定义是:给定一个背包的容量target,再给定一个数组nums表示物品,能否按照一定的方式选取nums中的元素得到target。
在解决实际问题的时候, 通常是将背包类型和问题类型做笛卡尔乘积,然后选择合适的算法。
按照背包类型进行分组:
| 背包类型 |
内层遍历顺序 |
例题 |
| 0-1 背包:每个元素只能使用一次 |
倒序遍历 |
给定背包容量,最多可以拿价值多少的物品 目标和问题 石头最小剩余的重量 |
| 完全背包问题:每个元素可以重复取 |
正序遍历 |
零钱兑换问题 |
| 组合背包问题:每个元素要求有序 |
正序遍历 |
|
| 分组背包:多个背包 (没见过) |
|
|
按照问题的类型进行分组:
| 问题类型 |
递推公式 |
例题 |
| 组合问题 |
dp[i]+=dp[i-num] |
目标和 |
| 最值问题 |
dp[i]=min/max(dp[i],dp[i-num]) |
剩余最少石头的数量 零钱兑换 完全平方数 |
| 存在性问题 |
`dp[i]=dp[i] |
|
股票买卖
股票买卖是一道用动态规划记录状态转移的问题
无法复制加载中的内容
K 次买卖
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| public int maxProfit(int[] prices) {
int n = prices.length;
int k = Math.min(k, n/2);
int[][][] dp = new int[n][k+1][2];
int ans=0;
for(int i=0;i<=k;i++){
dp[0][i][1] = -prices[0];
}
for(int i=1;i<n;i++){
for(int j=1;j<=k;j++){
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]);
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]);
ans = Math.max(dp[i][j][0], ans);
}
}
return ans;
}
|
N次买卖包含冷冻期
添加一个冷冻期的状态frozen;
卖出状态的前一天一定是冷冻期
冷冻期前一天可以是冷冻期或者买入状态
买入状态前一天可以是买入或者卖出状态
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| public int maxProfit(int[] prices) {
int n = prices.length;
int k = n/2;
int[][][] dp = new int[n][k+1][3];
int ans=0;
for(int i=0;i<=k;i++){
dp[0][i][1] = -prices[0];
}
for(int i=1;i<n;i++){
for(int j=1;j<=k;j++){
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]);
dp[i][j][2] = Math.max(dp[i-1][j][2], dp[i-1][j][1] + prices[i]);
dp[i][j][0] = dp[i-1][j][2];
ans = Math.max(Math.max(dp[i][j][0], dp[i][j][2]), ans);
}
}
return ans;
}
|
实际上,在进行无限次交易的时候,可以简化一下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][3];
int ans=0;
dp[0][0] = dp[0][2] = 0;
dp[0][1] = -prices[0];
for(int i=1;i<n;i++){
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
dp[i][2] = dp[i-1][1] + prices[i];
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2]);
ans = Math.max(dp[i][0], dp[i][2]);
}
return ans;
}
}
|
N次买卖包含手续费
除了状态转移方程外,其他与N次买卖相同:假设手续费为:fee
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
int ans=0;
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i=1;i<n;i++){
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
dp[i][0] = Math.max(dp[i-1][0], dp[i][1] + prices[i] - fee);
ans = Math.max(dp[i][0],ans);
}
return ans;
}
}
|
图 & 树
树:连通非循环无向图
- 搜索算法:BFS,DFS,拓扑排序
- 单元最短路径:Dijkstra,Floyd (要求图中没有环)
- 最小生成树:Kruskal 算法
递归回溯
力扣
DFS和回溯的区别
DFS是搜索算法,在搜索过程结束之后返回到上一层不会再多执行操作。而回溯算法在返回到上一层之后,会再次进行搜索。
DFS和回溯最大的区别是:有无状态重置。
何时使用回溯算法
当问题需要“回头”来找出所有解,即满足结束条件或者发现不是正确路径之后,要撤销选择,回退到上一个状态,继续尝试,直到找出所有解。
回溯算法的模板
例如,在子集问题中,给定一组不含重复元素的数组,返回所有可能的子集:
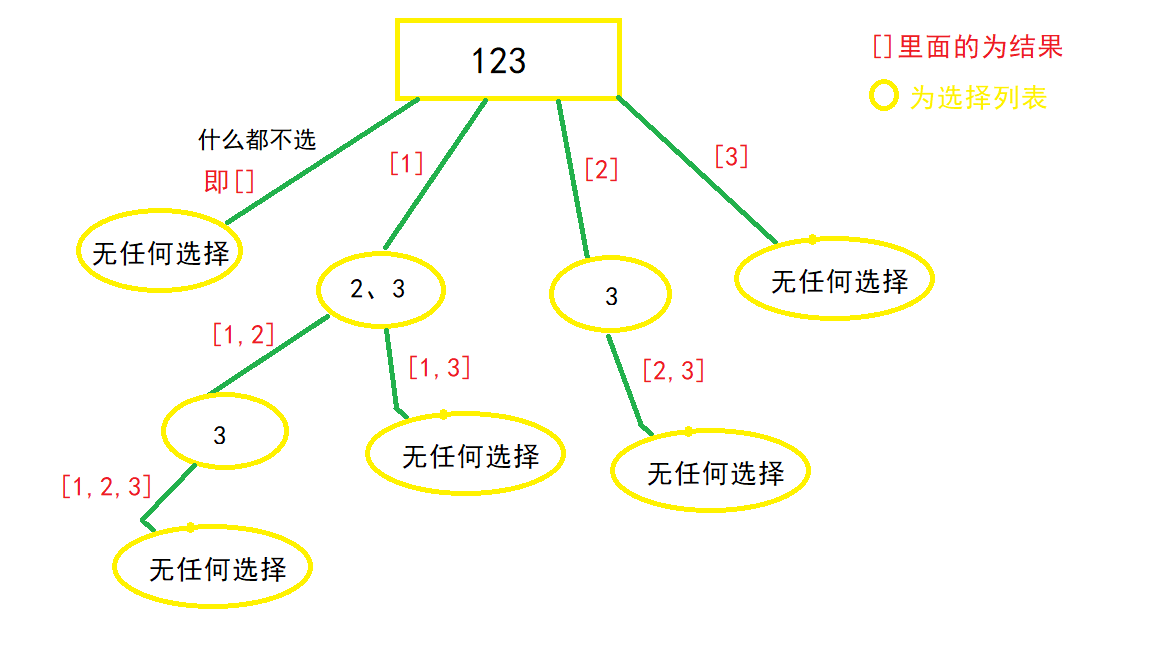
- 根据题意,确立结束条件
- 找准选择列表
- 判断是否需要剪枝
- 做出选择,递归调用,进入下一层
- 撤销选择
回溯问题的类型
回溯问题通常需要找到一个序列而不是总数(种类数),如果要求总数的话,可以使用背包来优化时间复杂度。因为回溯的时间复杂度是$$O(2^n)$$
| 类型 |
题目链接 |
| 子集、组合 |
LC78 子集1 LC90 子集2 |
| 全排列 |
LC46 全排列1 Lc47 全排列2 |
| 搜索 |
LC 79 单词搜索 N皇后 |
DFS
深度优先搜索,一种用于遍历搜索树或者图的算法,过程是对每一个可能的分支路径深入到不能深入为止,并且每个节点只能访问一次。
DFS的发明者在1986年获得图灵奖。
比较经典的例题:
- LC 111 二叉树深度
- LC 98 验证二叉搜索树
- LC 113 路径总和
排序算法
排序算法的任务简单,但是解决问题的思想非常经典。应用在快排、归并排序中的分治思想、递归实现在计算机的世界里有着广泛的应用。
注意:
很多算法题中不会直接考察排序算法,而是考察排序算法中的思想,比如:快排的Partition操作,计算逆序对和第K大元素等。

