SegmentQuery

区间问题

QuickView

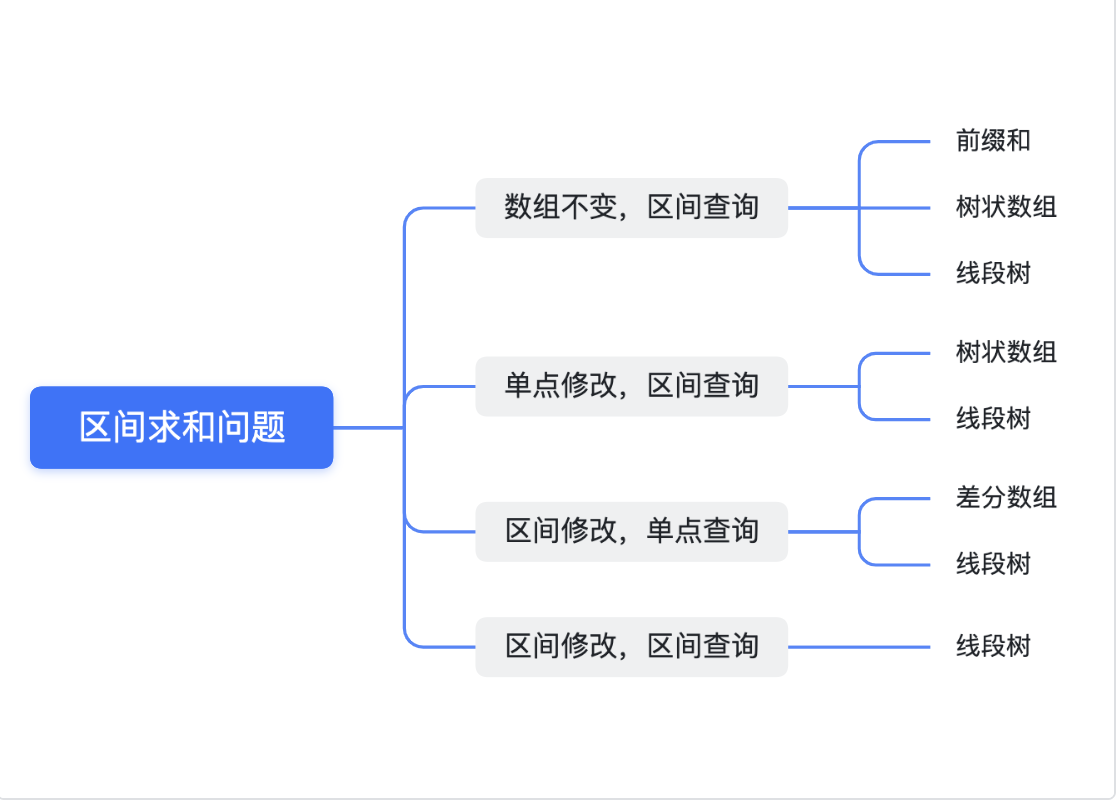
读者可以自行思考一个问题：对于一个数组 a，如果我想对 a 的进行以下三种操作，在不使用本文数据结构的情况下，暴力算法的时间复杂度为多少：

• 单点修改，区间查询：将第x个元素加k，求出 [x, y] 的区间和。

• 区间修改，单点查询：将 [x, y] 区域内的元素加k，并且求出第$ i (x <= i <= y) $个元素的值。

• 区间修改，区间查询：将 [x1, y1] 区域内的元素加k，并求出 [x2, y2] 的区间和

本文介绍数据结构

• 差分数组

• 树状数组

• 线段树

差分数组

定义：假设原数组为: a = int[]{2,5,7,3,6,9}，则差分数组b 的每一项为：
$$
b(i)=\left{ \begin{aligned} & a[i] - a[i-1], i > 0 \ & a[0], i=0 \ \end{aligned} \right.
$$
如下图所示。

index	0	1	2	3	4	5
a[i]	2	5	7	3	6	9
b[i]	2	3	2	-4	3	3

差分数组的性质

• 性质一：

求原数组中元素 a[i]，相当于求差分数组的前缀和
$$
a[i] = \sum_{j=0}^{i}b[j]
$$

• 性质二：

  • 求原数组中的前缀和：$\sum_{i=0}^{x}a[i] $，代入上式可得：

  • $\sum_{i=0}^{x}a[i] = \sum_{i=0}^{x}\sum_{j=0}^{i}b[j] = \sum_{i=0}^{x} (x-i+1)*b[i] $

  • 关于第二个等号，可以举个例子来说明：

  • 

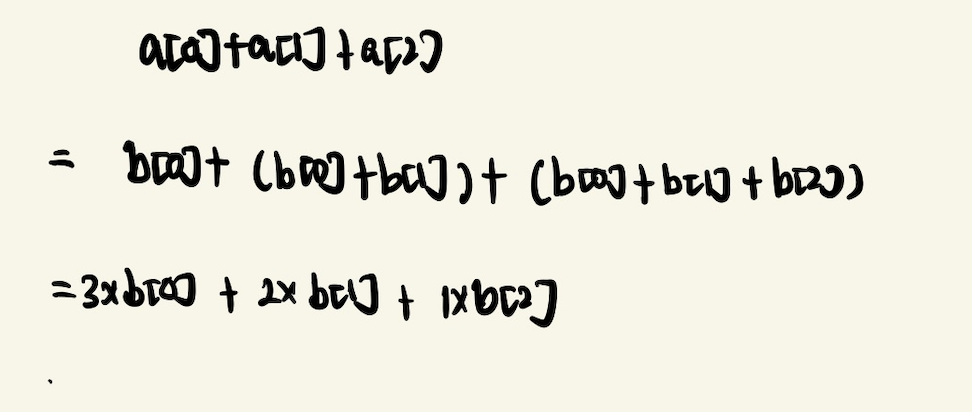
差分数组的用途

区间修改，区间查询

1. 快速处理区间修改操作

区间修改的操作可以分两步执行，例如对于操作给 [x, y] 区间加 K 这个操作：

• b[x] += K

• b[y+1] -= K

1. 快速处理区间查询问题

由性质二，可以在O(n) 的时间范围内查出原数组的前缀和；对于区间 [L, R] 的和为：

$SUM_{L, R} = SUM[R] - SUM[L-1] $

对于区间查询的问题，可以通过进一步地维护一个额外的空间来Trade-Off来压缩时间复杂度，感兴趣的读者可以自行了解。

树状数组

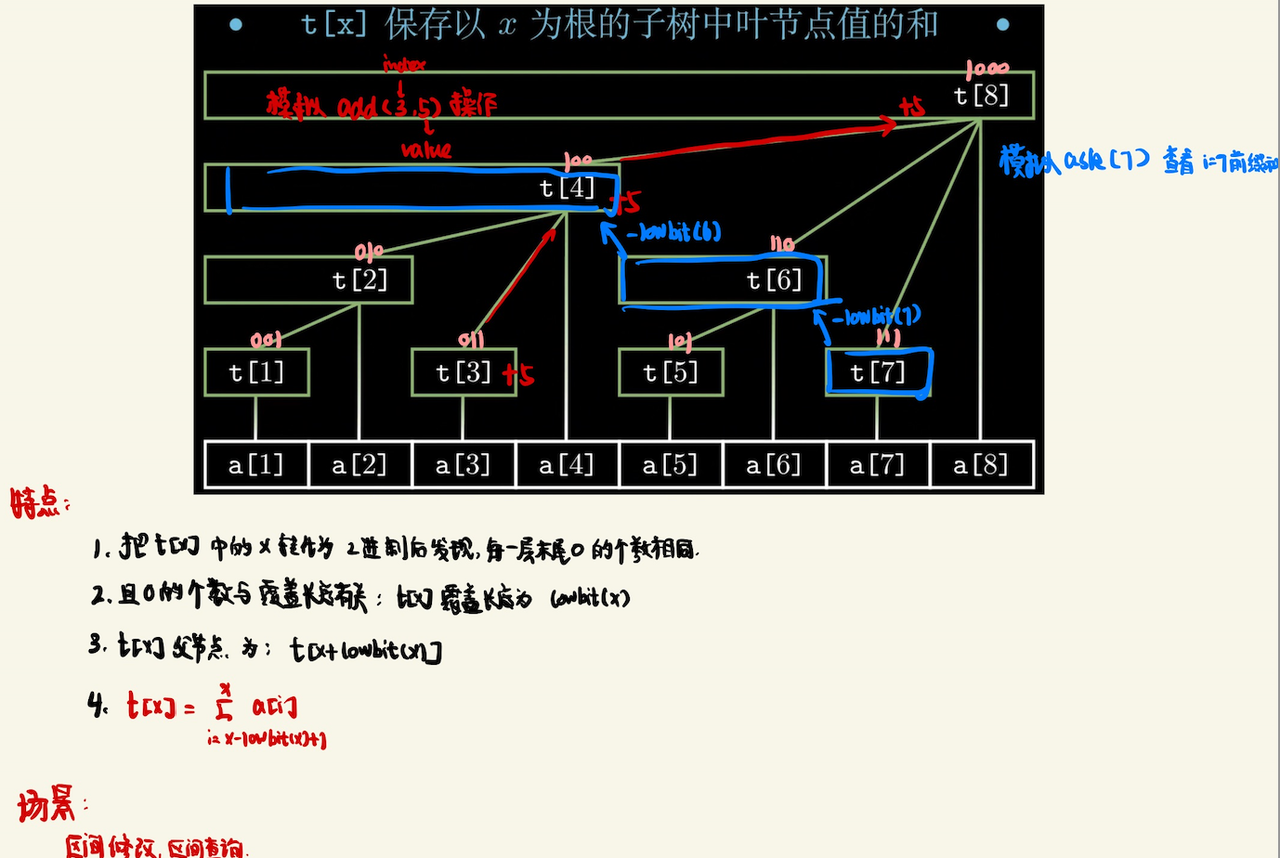
树状数组 t[x] 的每一个元素保存了以x为根节点的子树中叶子节点值的和，如下图所示。

Lowbit 操作

Lowbit(x): 表示x在二进制位表示下最低位的1及其之后的0构成的数值。如：

lowbit(44) = lowbit(0b101100) = (0b100) = 4

对于任意一个数 x 来说，它的lowbit值为：lowbit(x) = x & (-x)

性质

• 在t[x] 数组中，Lowbit(x) 表示了t[x] 覆盖的元素个数。

• t[x - lowbit(x)+1] 为 t[x] 覆盖原数组的第一个元素

• t[x + lowbit(x)] 为 t[x] 在树状数组中的父节点元素

使用场景

单点修改，区间查询

树状数组对于以下场景的计算具备良好的时间效率：

• 单点修改，区间查询，例如：修改 a[i]， 查询 $SUM_{L,R} $

反应到树状数组中，主要提供两个API：

Ask(x): Return the sum value from 0 to x
Add(x, k): Add k to x

对于Ask(x) 操作，从树状数组 t[x] 开始，往树的根节点方向寻找元素并相加，直到最顶层。伪代码如下：

sum := 0
for i:=x;i>0;i-=lowbit(i) {
    sum += t[i]
}

对于Add (x, K) 操作，从树状数组 t[x] 开始，往树的根节点方向寻找元素，并且把寻找到的每个元素值加 K，直到最顶层。

for i:=x;i<n;i+=lowbit(i){
    t[i] += K
}    

线段树

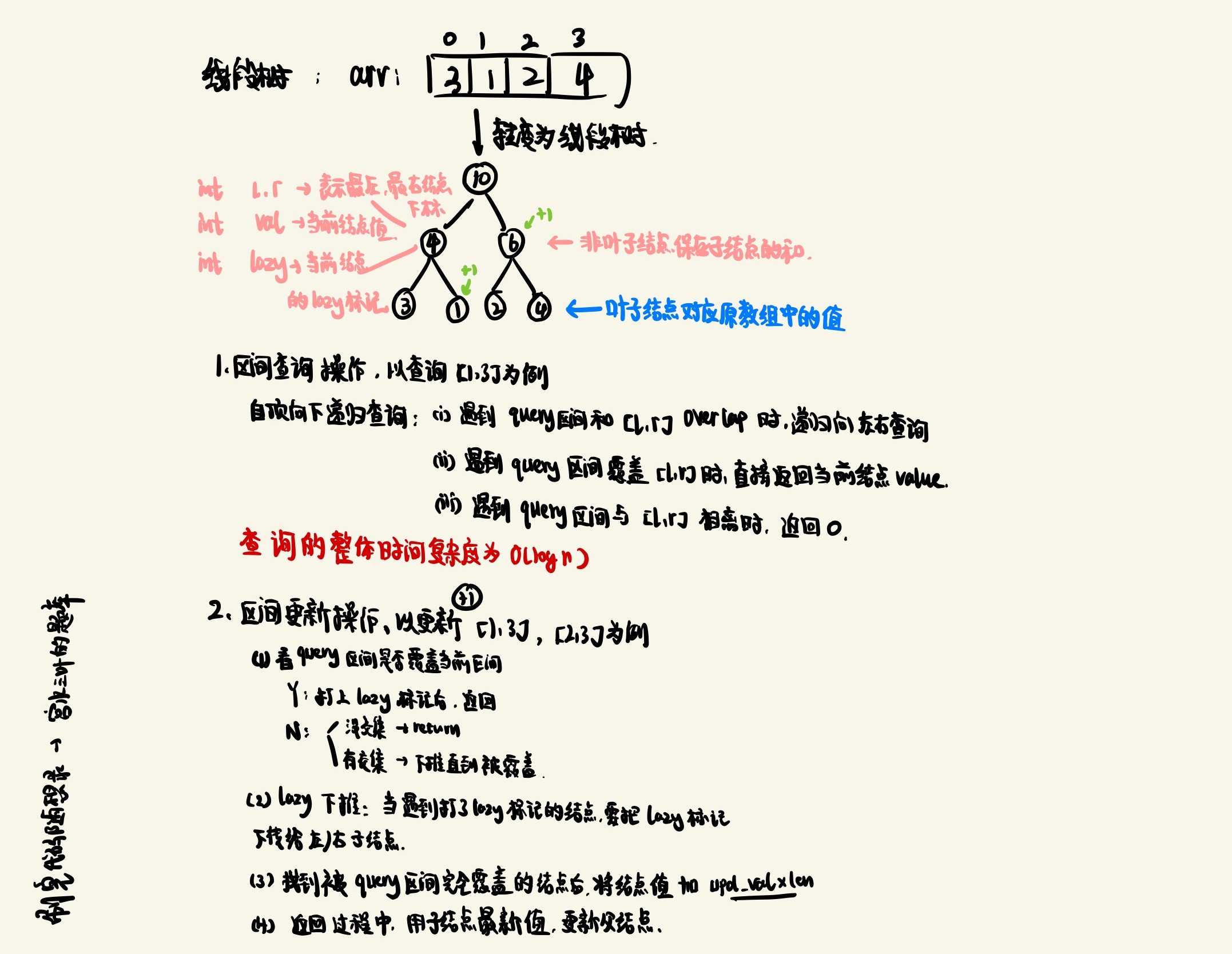
线段树解决的问题是：区间修改，区间查询。

线段树的每个叶子节点对应原数组中的值，每个非叶子节点表示子节点的节点值之和。

每个节点的数据结构如下：

struct TreeNode{
  left, right int // 表示当前节点覆盖的最左和最右节点的下标
  val int // 表示当前节点的节点值
  lazy int // lazy标记
}

区间查询的一般步骤为，自顶向下地递归查询：

1. 遇到query 区间和当前节点区间不相交的时候直接返回0；
2. 如果query 区间完全覆盖当前节点的区间，则直接返回当前节点的值；
3. 如果query 区间和当前节点的区间相交，则向下寻找被完全覆盖的节点并且返回该节点的值。

区间更新的操作为

大体包括四个步骤：判断是否覆盖 -> 看是否有lazy标记 -> lazy标记下推 -> 更新左右节点 -> 更新父节点

1. 如果Query 区间完全覆盖当前区间则给当前区间打上Lazy标记后返回，回溯的过程中更新父节点的值；
2. 如果Query 区间完全覆盖的区间上有lazy标记，则将lazy标记下推，下推的操作是将当前的lazy操作应用到两个子节点上，然后返回，回溯的过程中更新父节点的值；

使用场景的总结

可能帮助你理解的例子

732. 我的日程安排表 III

1109. 航班预订统计

For More Information: SharingSource